7. Sampling and Reconstruction
Radiance在胶平面上是连续函数,但是渲染的输出是离散的像素。
But what happens when we need the value of s signal at a location that we didn’t sample at? In such cases, we can use a process known as reconstruction to derive an approximation of the original continuous function. With this approximation we can then discretely sample its values at a new set of sample points, which is referred to as resampling. signal processing primer
7.1 Sampling Theory
- 7.1.1 The Frequency Domain and the Fourier Transform
Definition
of the Fourier (and Inverse) Transform (synthesis and analysis)
 书里给的是第二种定义方式
书里给的是第二种定义方式Symmetric Form: Hertz Frequency
- 7.1.2 Ideal Sampling and Reconstruction 使用shah fucntion、impulse
train function也叫Dirac comb,记作
来乘以函数来进行采样。
采样过程如下:
有个疑问,对于Dirac delta函数
采样:

重建:
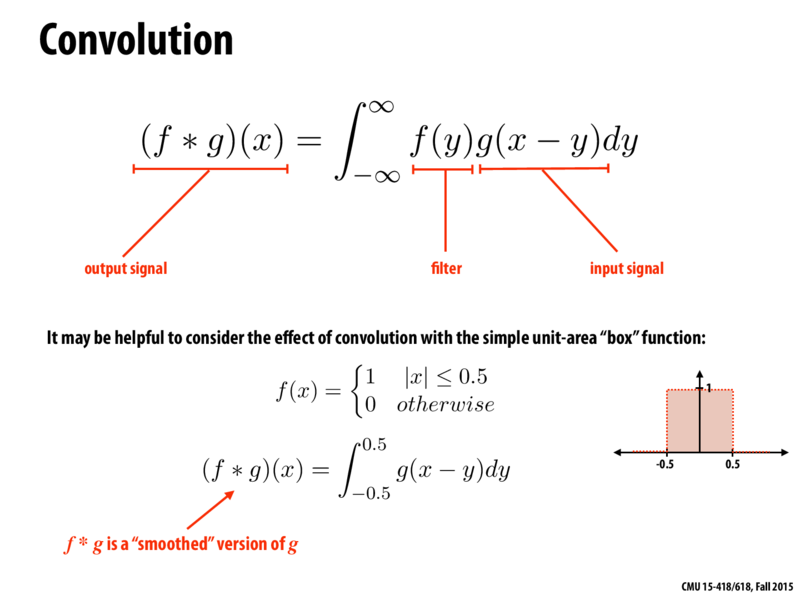

来自the dirac comb and its fourier transform
An important idea used in Fourier analysis is the fact that the Fourier transform of the product of two functions
can be shown to be the convolution of their individual Fourier transforms and : . It is similarly the case that convolution in the spatial domain is equivalent to multiplication in the frequency domain:
空域的周期和频域的周期互为相反数,这是理解混叠的关键,空域中采样间隔越大,在频域中间隔就越小,就导致频域的互相挤压,一起混叠(aliasing)。
the Fourier transform of a shah function with period
is another shah function with period . This reciprocal relationship between periods is important to keep in mind: it means that if the samples are farther apart in the spatial domain, they are closer together in the frequency domain.
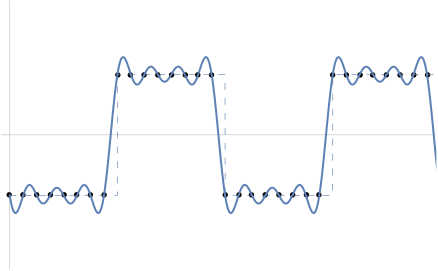
- 7.1.4 Antialiasing Techniques
NonUniform Sampling
以前是在整数倍周期位置采样,现在在整数倍附近
- 7.1.7 Understanding Pixels
- Pixel是图像函数上的采样点,并不关联面积的概念。
- 图像定义再离散坐标
上,采样函数定义在连续浮点型坐标 位置上,(这里的离散值应该是离散的序号,连续值是物理意义的位置,可以映射,但是不能等同)。可以使用不同的映射,1)取整到最近的整数,即离散点正好落在整数位置上,2)向下取整,即离散点落在整数点距离0.5的位置。
7.2 Sampling Interface
- Evaluating Sample Patterns: Discrepancy
- 使用
discrepancy评估采样样式的质量。采样范围, discrepancy的定义如下: Note
“sup”是数学中常用的符号,代表“上确界”(supremum)。它表示一个集合或函数的最小上界。
Note
“sup”是数学中常用的符号,代表“上确界”(supremum)。它表示一个集合或函数的最小上界。 - 采样点的聚集性,使用点之间的最小距离来度量。
Sobol采样器就存在采样点集中聚集的问题,太近的采样点能提供的额外信息更少
Intuitively, samples that are too close together aren’t a good use of sampling resources: the closer one sample is to another, the less likely it is to give useful new information about the function being sampled. Therefore, computing the minimum distance between any two samples in a set of points has also proved to be a useful metric of sample pattern quality; the higher the minimum distance, the better.
Poisson disk sampling采样模式在距离度量上表现优异。Studies
have shown that the rods and cones in the eye are distributed in a
similar way, which further validates the idea that this distribution is
a good one for imaging.
实际使用中,Poisson disk sampling更适合2D图像的采样,在更高维采样时就没那么有效了。
- 实现
- Pixel Sampler:一次性生成一个像素的所有采样值
- Global Sampler:顺序的为一张图的每个像素点生成一个采样值,每次访问不同的像素位置,比如HaltonSampler、SobelSampler
7.3 Stratified Sampling
采样的每一维作划分,然后通过jittering每一个stratum的中心确定采样点。
> The key idea behind stratification is that by subdividing the
sampling domain into nonoverlapping regions and taking a single sample
from each one, we are less likely to miss important features of the
image entirely, since the samples are guaranteed not to all be close
together.
直接应用分层采样于高维的采样空间,势必要采样数量几何爆炸。实际中并不需要这么费力不讨好,可以把多维采样空间划分为多个子集,在低维度应用分层采样,最后把各个子集的采样点随意组合起来,这样就可以不必要付出过量的完整采样代价,也能获得分层采样的效果。
> We can reap most of the benefits of stratification without paying
the price in excessive total sampling by computing lower dimensional
stratified patterns for subsets of the domain’s dimensions and then
randomly associating samples from each set of dimensions. (This process
is sometimes called padding.) 这句话太长了。。。难懂~~
采样数组的两个目标:良好分布到采样空间;采样之间的数值不要太相似。
如果采样数不是平方数(影响第二个目标),stratification就不太好应用。把采样数舍入到最近的平方数或可一用,但是Latin
hypercube sampling (LHS),也叫n-rooks
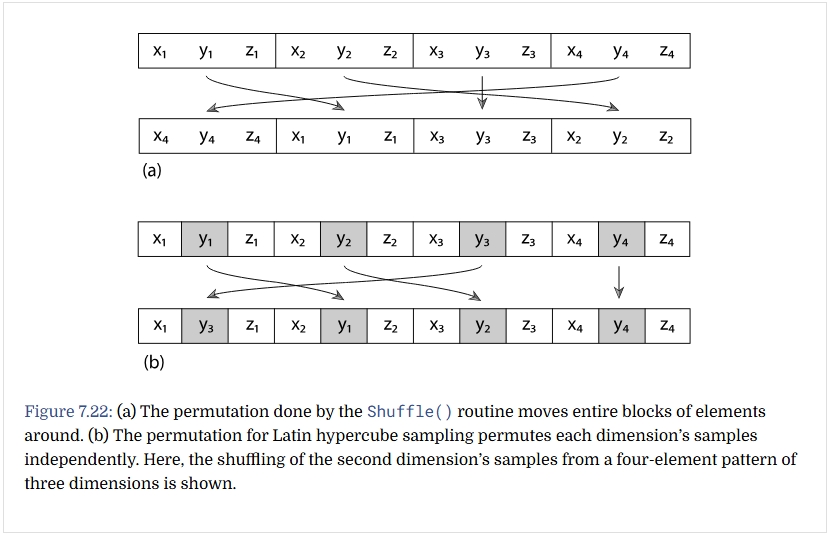
sampling,更适合。在每个采样维度上平均划分n各区域,沿着采样空间对角线上的n个小区域,使用jitter生成n个采样,再对采样进行shuffle重排。普通的重排是采样的多个维的整体重排,LHS的重排是多个维分别重排。
7.4 The Halton Sampler
StratifiedSampler优缺点:well-distributed but
non-uniform,
采样点不会太近且不会发生足够大的区域内没有采样点的情形。如果两个strata内的jitter采样点都靠近共享边,采样质量就比较糟糕。
HaltonSampler直接生成low-discrepancy的点集,保证点不聚集,且在每一维上都良好分布。
radical inverse

van der Corput sequence
1D sequence given by the radical inverse function in base 2:
n-dimensional Halton sequence
每维序列生成radical_inverse使用的base是前n个素数
Hammersley 当N固定时,更低的discrepancy。
参考Sampling with Hammersley and Halton Points
scrambled Halton and Hammersley
随着base底的增加,Halton and
Hammersley采样序列会呈现严重的规则样式,解决方法对radical
inverse的数字进行重排